The Rayleigh Criterion for Microscope Resolution
The lateral (X-Y) resolution of fluorescence and Raman microscopes is frequently calculated using the famous Rayleigh Criterion for resolution, 0.61λ/NA, but where does this resolution limit arise from and how does it relate to the other resolution limits encountered in microscopy?
The Point Spread Function & Airy Pattern
When a point emitter (such as a quantum dot) is imaged by a microscope, its image is blurred due to diffraction. The diffraction pattern of a point emitter in the image plane of a microscope is described by the 2D point spread function (PSF). For a perfect imaging system with no aberrations, this pattern is also known as the Airy pattern and is shown in Figure 1. It consists of a bright central circle, the Airy disc, which contains 84% of the total light intensity, with the remaining 16% distributed across a series of progressively less intense concentric rings. The size of the Airy disc is given by:

Where λ is the wavelength of the emitted or scattered light and NA is the numerical aperture of the microscope’s objective lens. NA is a measure of the objective’s ability to capture light and is the product of the sine of the half-angle of the objective’s acceptance cone, α, and the refractive index, n, of the medium between the sample and objective lens:
![]()
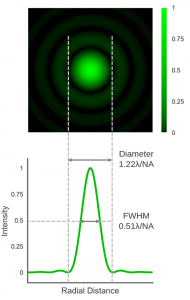
Figure 1 2D-Point Spread Function / Airy Pattern of a point emitter.
What is Resolution?
Resolution can be defined as the minimum separation between two objects that results in a certain level of contrast between them. When two objects are brought together their PSFs combine additively and the total PSF of both objects is what is imaged by the microscope. When the objects are sufficiently far apart there is a dip in the intensity of the total PSF between the objects and they can be distinguished as separate entities and said to be resolved. The various microscopy lateral resolution limits, of which the Rayleigh criterion is but one, are essentially just different definitions of what constitutes a sufficient level of contrast between the objects for them to be resolved.
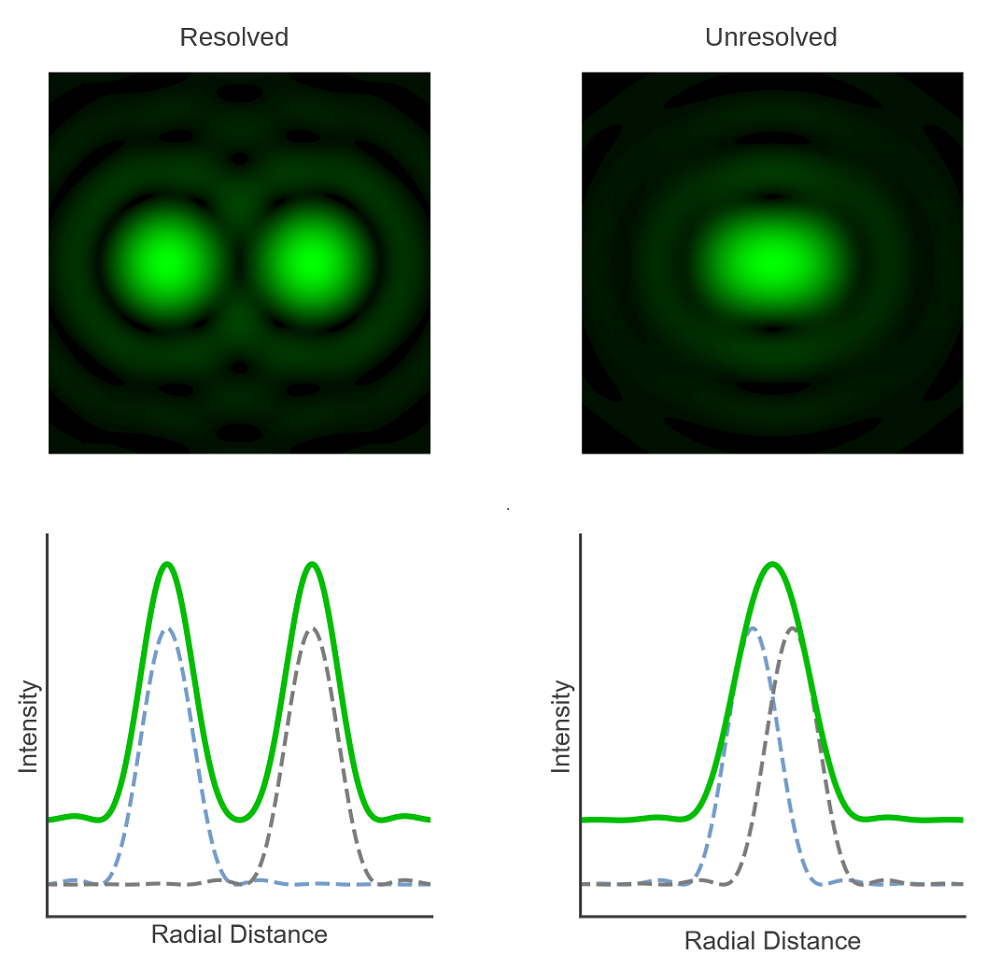
Figure 2: Overlap of PSFs and resolution of two point emitters at different radial distances.
Rayleigh Criterion
The Rayleigh criterion is named after English physicist John William Strutt, 3rd Baron Rayleigh (1842-1919) who investigated the image formation of telescopes and microscopes in the late 19th century. Rayleigh defined the resolution limit as the separation where the central maximum of the Airy pattern of one point emitter is directly overlapping with the first minimum of the Airy pattern of the other.1,2 In other words, the minimum resolvable separation between the points is the radius of the Airy disc which is given by:

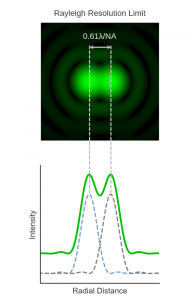
Figure 3 Two points separated by the Rayleigh resolution limit.
Rayleigh chose his criterion based on the human visual system and to provide sufficient contrast for an observer to distinguish two separate objects in the image. The Rayleigh criterion is therefore not a fundamental physical law and instead a somewhat arbitrarily defined value. This was clearly stated by Rayleigh himself in 1879:2
This rule is convenient on account of its simplicity; and it is sufficiently accurate in view of the necessary uncertainty as to what exactly is meant by resolution.
This does not make it any less useful and the Rayleigh criterion has become one of the most ubiquitous definitions of microscope resolution.
Sparrow Limit
The Sparrow limit is a less commonly encountered resolution limit proposed by the American physicist Carrol Mason Sparrow (1880 – 1941) in 1916.3 Sparrow’s limit is defined as the separation between two point emitters when the total PSF has no dip in intensity at the midpoint and there is instead an intensity plateau between the points. The Sparrow limit is, therefore, smaller than that defined by Rayleigh and is given by:

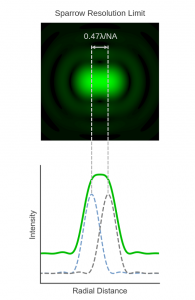
Figure 5 Two points separated by the Sparrow resolution limit.
Abbe Limit
Ernst Abbe (1840 – 1905), was a German physicist who made pioneering contributions to the design and theory of optical microscopy. He was a research director at Zeiss Optical Works (now ZEISS) and introduced the concept of numerical aperture to describe optical systems. In 1873 Abbe published his seminal paper on image formation in microscopes, “Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung” (Contributions to the Theory of the Microscope and the Nature of Microscopic Vision).4 The original paper is in German but a modern English translation can be found in Barry R. Masters book on super-resolution microscopy.5 Abbe’s 1873 paper is unusual in that it contained not a single equation. In it, Abbe profoundly stated that microscope resolution is determined by the wavelength of light the numerical aperture of the objective, and this was later formulated into the equation now known as the Abbe limit for resolution:
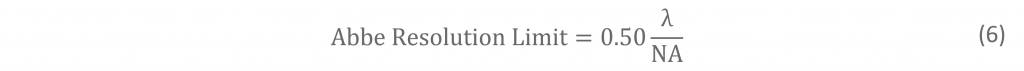
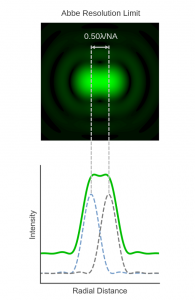
Figure 4 Two points separated by the Abbe resolution limit.
FWHM
A more practical definition of microscope resolution is to use the FWHM of the point spread function (see Figure 1) which has a theoretical minimum value of:
![]()
The advantage of using the FWHM is that it can be easily measured in the lab by imaging a pseudo point emitter (such as a sub-resolution fluorescent bead) and therefore be used as a comparison metric for real microscope systems – in contrast to the other limits which are theoretical ideals.
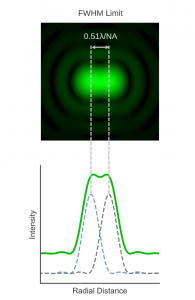
Figure 6 Two points separated by the FWHM.
The RM5 Raman Microscope
If you are working in the field of Raman Spectroscopy, our Raman Confocal Microscope may be the perfect partner for your Raman research.
For further information please Contact Us.
Keep in Touch
If you have enjoyed reading this article, why not sign up to our monthly newsletter via the button below or follow us on LinkedIn, Twitter or Facebook to keep up to date with our latest news and research.
References
1. L. Rayleigh, On the theory of optical images, with special reference to the microscope. London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 42, Part XV, 167–195 (1896)
2. L. Rayleigh, Investigations in optics, with special reference to the spectroscope. London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 8, Part XXXI, 261–274 (1879)
3. C. M. Sparrow. On spectroscopic resolving power. Astrophysical Journal, 44, 76–86 (1916)
4. E. Abbe, Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. Archiv für mikroskopische Anatomie, IX, 413–468 (1873)
5. R. Masters, Superresolution Optical Microscopy, Springer Series in Optical Sciences (2020)








